Evolving Neural Networks Through Augmenting Topologies

Python Implementation of NEAT Genetic Algorithm

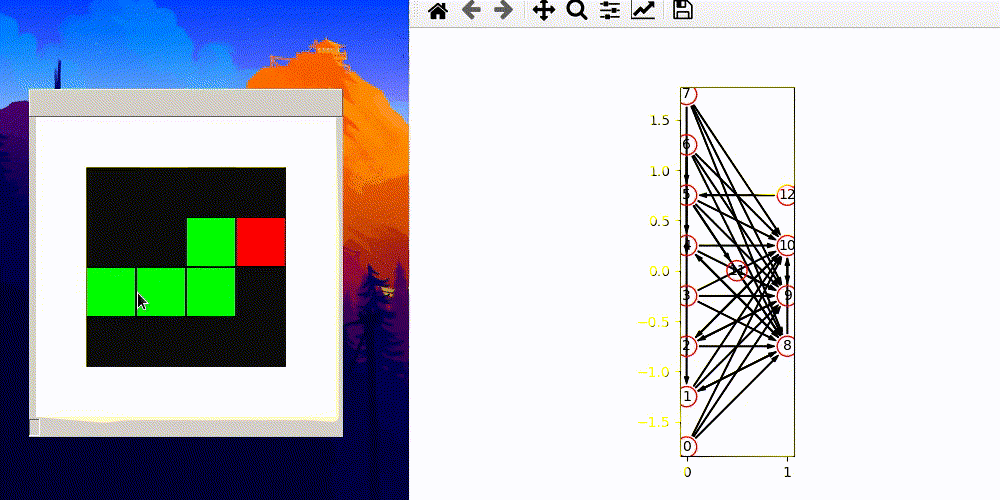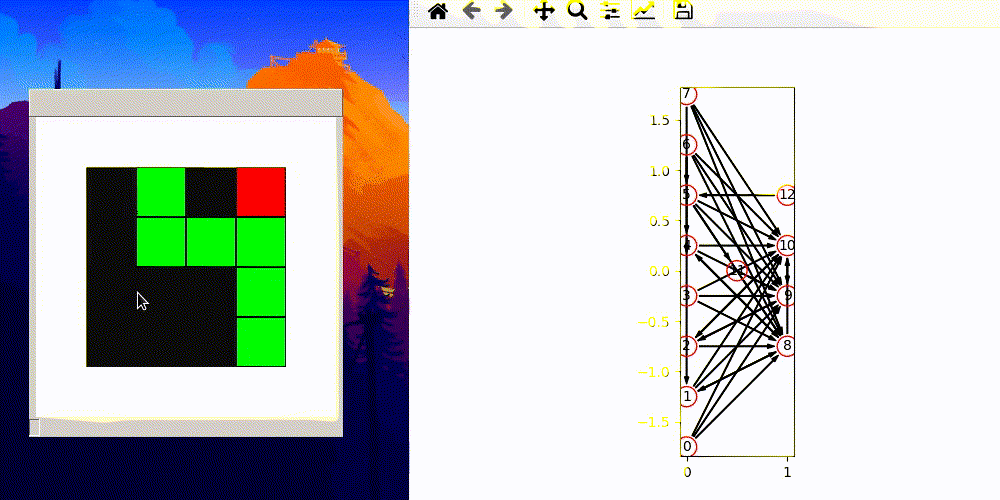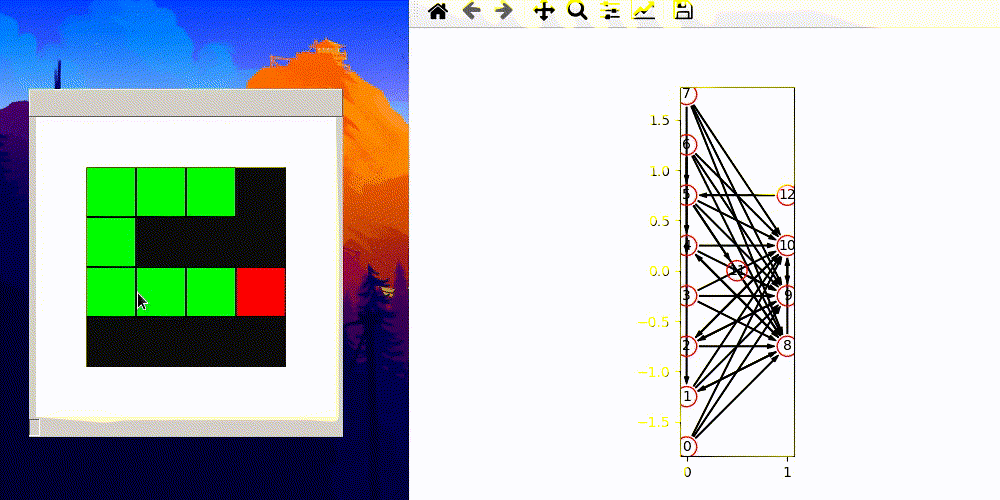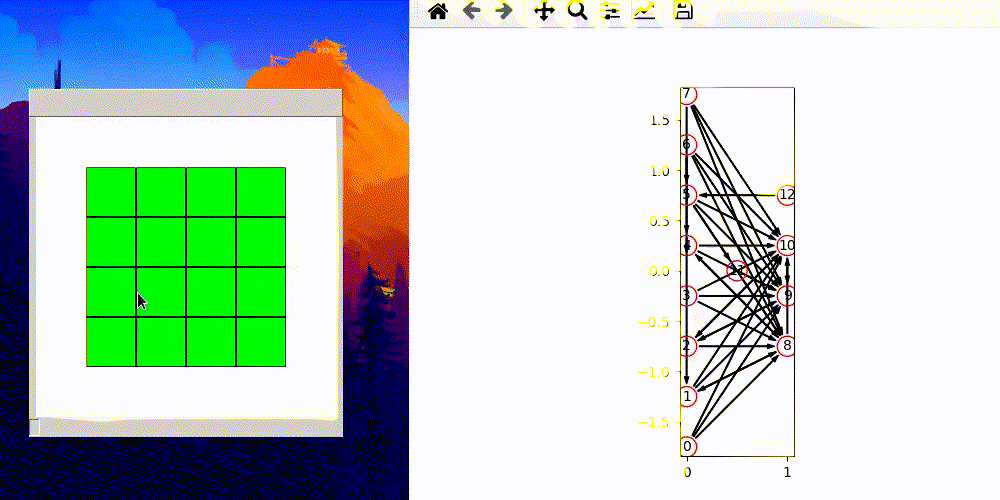
Above gif was pure luck and it is from an earlier version which allows connection to inputs and connection from outputs.

Requirements

• Python >= 3.6

Optional

• Matplotlib (To draw genomes)

Gym Examples

• gym
• mpi4py (Parallel NEAT Example)

Snake Example

• snake
• numpy
• cv2

Install

git clone https://github.com/goktug97/NEAT
cd NEAT
python3 setup.py install --user

Usage

xor.py

import neat
xor = neat.NEAT(n_networks = 150,
                input_size = 2,
                output_size = 1,
                bias = True,
                c1 = 1.0, c2 = 1.0, c3 = 0.4,
                distance_threshold = 3.0,
                weight_mutation_rate = 0.8,
                node_mutation_rate = 0.03,
                connection_mutation_rate = 0.05,
                interspecies_mating_rate = 0.001,
                disable_rate = 0.75,
                stegnant_threshold = 15,
                input_activation = neat.steepened_sigmoid,
                hidden_activation = neat.steepened_sigmoid,
                output_activation = neat.steepened_sigmoid)
truth_table = [[0, 1],[1, 0]]
solution_found = False
while True:
    print(f'Generation: {xor.generation}')
    rewards = []
    for genome in xor.population:
        error = 0
        for input_1 in range(len(truth_table)):
            for input_2 in range(len(truth_table[0])):
                output = int(round(genome([input_1, input_2])[0]))
                error += abs(truth_table[input_1][input_2] - output)
        fitness = (4 - error) ** 2
        rewards.append(fitness)
        if fitness == 16:
            solution_found = True
            break
    if solution_found:
        break
    xor.next_generation(rewards)
import matplotlib.pyplot as plt
genome.draw()
plt.show()

• Parallel Bipedal Example
• Gym Cartpole Example
• Snake Example

References

• Kenneth O. Stanley, , and Risto Miikkulainen. “Evolving Neural Networks Through Augmenting Topologies”.Evolutionary Computation 10, no.2 (2002): 99-127.