Effect of hidden nodes on the reconstruction on bidirectional networks

Emily S. C Ching, P. H. Tam, “Effects of hidden nodes on the reconstruction of bidirectional networks“, Phys. Rev. E 98, 062318 (2018)

To demonstrate the method used in this journal publication using Python.

Prerequisite

1. Python 3 intepreter
2. Jupyter Notebook
3. numpy
4. sklearn
5. matplotlib
6. tqdm

pip -r install requirements.txt

Project Structure

1. Demo.ipynb
   
   Jupyter notebook to demonstrate network reconstruction

2. utils
   
   A package with general tools for computations

3. gen_net
   
   A package to generate weighted adjacency matrix from a network model

4. gen_cov
   
   A package to generate covariance matrix from a dynamical system given the weighted adjacency matrix

5. choose_nodes
   
   A package to select nodes as measured nodes and hidden nodes

6. reconstruct
   
   A package to reconstruct adjacency matrix from a reconstruction method given the data

7. evaluate
   
   A package to evaluate the reconstruction performance

8. plots
   
   A package to plot figures

Dynamics

The above figure shows one of the nodal dynamics. It fluctuates around a stable fixed point (red dotted line). The time series is sampled after the green dotted line for covariance computation. This network consists of 100 nodes in total.

Data Distribution

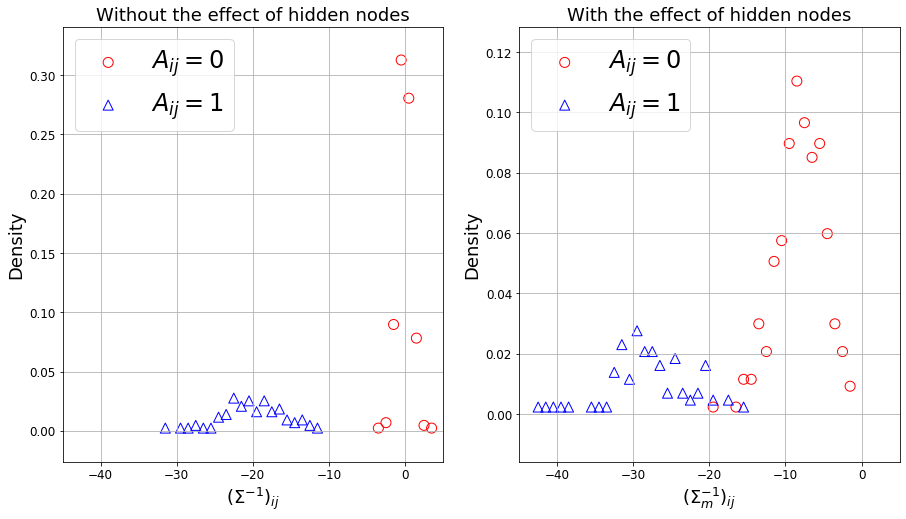
1. Left: Without effect of hidden node. A bimodal distribution is observed with unconnected data points around zero.

2. Right: With effect of hidden node. A bimodal distribution is still observed even if there are 70 out of 100 nodes are hidden nodes. What is remarkable is that when you compare with the Left figure, it is as if the whole distribution is shifted to the left by roughly the same amount without distorting the bimodal feature.

3. Notice that we are using inverse covariance matrix not the covariance matrix itself to reconstruct the network connectivity. See also Reconstructing weighted networks from dynamics and Reconstructing networks from dynamics with correlated noise

Citation

@article{PhysRevE.98.062318,
  title = {Effects of hidden nodes on the reconstruction of bidirectional networks},
  author = {Ching, Emily S. C. and Tam, P. H.},
  journal = {Phys. Rev. E},
  volume = {98},
  issue = {6},
  pages = {062318},
  numpages = {9},
  year = {2018},
  month = {Dec},
  publisher = {American Physical Society},
  doi = {10.1103/PhysRevE.98.062318},
  url = {https://link.aps.org/doi/10.1103/PhysRevE.98.062318}
}